In a certain city, age is reckoned in terms of real numbers rather than integers. Every two citizens  and
and 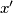 either know each other or do not know each other. Moreover, if they do not, then there exists a chain of citizens
either know each other or do not know each other. Moreover, if they do not, then there exists a chain of citizens 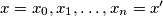 for some integer
for some integer  such that
such that 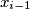 and
and 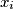 know each other. In a census, all male citizens declare their ages, and there is at least one male citizen. Each female citizen provides only the information that her age is the average of the ages of all the citizens she knows. Prove that this is enough to determine uniquely the ages of all the female citizens.
know each other. In a census, all male citizens declare their ages, and there is at least one male citizen. Each female citizen provides only the information that her age is the average of the ages of all the citizens she knows. Prove that this is enough to determine uniquely the ages of all the female citizens.
 and
and 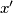 either know each other or do not know each other. Moreover, if they do not, then there exists a chain of citizens
either know each other or do not know each other. Moreover, if they do not, then there exists a chain of citizens 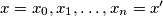 for some integer
for some integer  such that
such that 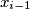 and
and 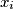 know each other. In a census, all male citizens declare their ages, and there is at least one male citizen. Each female citizen provides only the information that her age is the average of the ages of all the citizens she knows. Prove that this is enough to determine uniquely the ages of all the female citizens.
know each other. In a census, all male citizens declare their ages, and there is at least one male citizen. Each female citizen provides only the information that her age is the average of the ages of all the citizens she knows. Prove that this is enough to determine uniquely the ages of all the female citizens.  Školjka
Školjka