There are 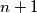 cells in a row labeled from
cells in a row labeled from 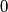 to
to  and
and 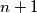 cards labeled from
cards labeled from 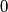 to
to  . The cards are arbitrarily placed in the cells, one per cell. The objective is to get card
. The cards are arbitrarily placed in the cells, one per cell. The objective is to get card  into cell
into cell  for each
for each  . The allowed move is to find the smallest
. The allowed move is to find the smallest 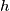 such that cell
such that cell 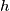 has a card with a label
has a card with a label  , pick up that card, slide the cards in cells
, pick up that card, slide the cards in cells 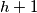 ,
, 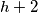 , ... ,
, ... ,  one cell to the left and to place card
one cell to the left and to place card  in cell
in cell  . Show that at most
. Show that at most 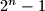 moves are required to get every card into the correct cell and that there is a unique starting position which requires
moves are required to get every card into the correct cell and that there is a unique starting position which requires 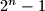 moves. [For example, if $n = 2$ and the initial position is 210, then we get 102, then 012, a total of 2 moves.]
moves. [For example, if $n = 2$ and the initial position is 210, then we get 102, then 012, a total of 2 moves.]
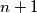 cells in a row labeled from
cells in a row labeled from 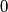 to
to  and
and 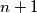 cards labeled from
cards labeled from 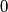 to
to  . The cards are arbitrarily placed in the cells, one per cell. The objective is to get card
. The cards are arbitrarily placed in the cells, one per cell. The objective is to get card  into cell
into cell  for each
for each  . The allowed move is to find the smallest
. The allowed move is to find the smallest 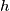 such that cell
such that cell 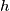 has a card with a label
has a card with a label  , pick up that card, slide the cards in cells
, pick up that card, slide the cards in cells 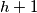 ,
, 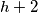 , ... ,
, ... ,  one cell to the left and to place card
one cell to the left and to place card  in cell
in cell  . Show that at most
. Show that at most 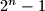 moves are required to get every card into the correct cell and that there is a unique starting position which requires
moves are required to get every card into the correct cell and that there is a unique starting position which requires 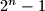 moves. [For example, if $n = 2$ and the initial position is 210, then we get 102, then 012, a total of 2 moves.]
moves. [For example, if $n = 2$ and the initial position is 210, then we get 102, then 012, a total of 2 moves.]  Školjka
Školjka