Let 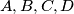 be four distinct points on a line, in that order. The circles with diameters
be four distinct points on a line, in that order. The circles with diameters  and
and  intersect at
intersect at  and
and  . The line
. The line  meets
meets  at
at  . Let
. Let  be a point on the line
be a point on the line  other than
other than  . The line
. The line 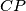 intersects the circle with diameter
intersects the circle with diameter  at
at  and
and  , and the line
, and the line 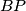 intersects the circle with diameter
intersects the circle with diameter  at
at  and
and  . Prove that the lines
. Prove that the lines 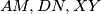 are concurrent.
are concurrent.
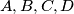 be four distinct points on a line, in that order. The circles with diameters
be four distinct points on a line, in that order. The circles with diameters  and
and  intersect at
intersect at  and
and  . The line
. The line  meets
meets  at
at  . Let
. Let  be a point on the line
be a point on the line  other than
other than  . The line
. The line 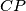 intersects the circle with diameter
intersects the circle with diameter  at
at  and
and  , and the line
, and the line 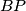 intersects the circle with diameter
intersects the circle with diameter  at
at  and
and  . Prove that the lines
. Prove that the lines 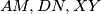 are concurrent.
are concurrent.  Školjka
Školjka