Let
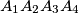
be a tetrahedron,

its centroid, and
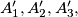
and
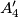
the points where the circumsphere of
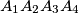
intersects
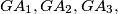
and
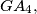
respectively. Prove that
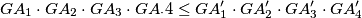
and
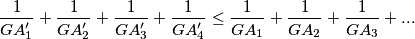
%V0
Let $A_1A_2A_3A_4$ be a tetrahedron, $G$ its centroid, and $A'_1, A'_2, A'_3,$ and $A'_4$ the points where the circumsphere of $A_1A_2A_3A_4$ intersects $GA_1,GA_2,GA_3,$ and $GA_4,$ respectively. Prove that
$$GA_1 \cdot GA_2 \cdot GA_3 \cdot GA_ \cdot4 \leq GA'_1 \cdot GA'_2 \cdot GA'_3 \cdot GA'_4$$
and
$$\frac{1}{GA'_1} + \frac{1}{GA'_2} + \frac{1}{GA'_3} + \frac{1}{GA'_4} \leq \frac{1}{GA_1} + \frac{1}{GA_2} + \frac{1}{GA_3} +...$$