Slični zadaci
Let 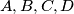 be four distinct points on a line, in that order. The circles with diameters
be four distinct points on a line, in that order. The circles with diameters  and
and  intersect at
intersect at  and
and  . The line
. The line  meets
meets  at
at  . Let
. Let  be a point on the line
be a point on the line  other than
other than  . The line
. The line 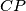 intersects the circle with diameter
intersects the circle with diameter  at
at  and
and  , and the line
, and the line 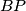 intersects the circle with diameter
intersects the circle with diameter  at
at  and
and  . Prove that the lines
. Prove that the lines 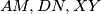 are concurrent.
are concurrent.
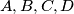 be four distinct points on a line, in that order. The circles with diameters
be four distinct points on a line, in that order. The circles with diameters  and
and  intersect at
intersect at  and
and  . The line
. The line  meets
meets  at
at  . Let
. Let  be a point on the line
be a point on the line  other than
other than  . The line
. The line 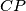 intersects the circle with diameter
intersects the circle with diameter  at
at  and
and  , and the line
, and the line 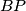 intersects the circle with diameter
intersects the circle with diameter  at
at  and
and  . Prove that the lines
. Prove that the lines 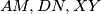 are concurrent.
are concurrent.  Školjka
Školjka  be a positive integer. Show that there are infinitely many perfect squares of the form
be a positive integer. Show that there are infinitely many perfect squares of the form 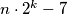 where
where  is a positive integer.
is a positive integer.  and
and  be non-negative integers such that
be non-negative integers such that 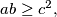 where
where  is an integer. Prove that there is a number
is an integer. Prove that there is a number 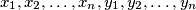 such that
such that 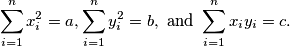
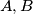 and
and  such that
such that 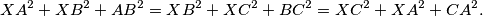
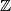 denote the set of all integers. Prove that for any integers
denote the set of all integers. Prove that for any integers  and
and  one can find an integer
one can find an integer 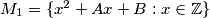 and
and 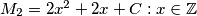 do not intersect.
do not intersect. 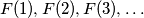 of non-negative integers that simultaneously satisfies the following three conditions?
of non-negative integers that simultaneously satisfies the following three conditions? 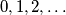 occurs in the sequence.
occurs in the sequence. 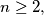
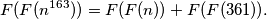
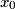 for which there exists a sequence
for which there exists a sequence 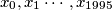 of positive reals with
of positive reals with 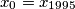 , such that
, such that 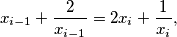
 .
.