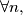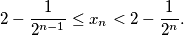Slični zadaci
An acute triangle  is given. Points
is given. Points  and
and  are taken on the side
are taken on the side  (with
(with  between
between  and
and  ),
),  and
and  on the side
on the side  (with
(with  between
between  and
and  ), and
), and  and
and 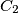 on the side
on the side  (with
(with 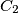 between
between  and
and  ) so that
) so that
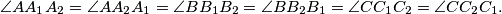
The lines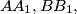 and
and 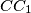 bound a triangle, and the lines
bound a triangle, and the lines 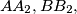 and
and 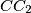 bound a second triangle. Prove that all six vertices of these two triangles lie on a single circle.
bound a second triangle. Prove that all six vertices of these two triangles lie on a single circle.
 is given. Points
is given. Points  and
and  are taken on the side
are taken on the side  (with
(with  between
between  and
and  ),
),  and
and  on the side
on the side  (with
(with  between
between  and
and  ), and
), and  and
and 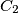 on the side
on the side  (with
(with 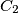 between
between  and
and  ) so that
) so that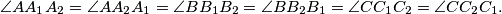
The lines
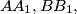 and
and 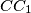 bound a triangle, and the lines
bound a triangle, and the lines 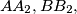 and
and 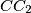 bound a second triangle. Prove that all six vertices of these two triangles lie on a single circle.
bound a second triangle. Prove that all six vertices of these two triangles lie on a single circle.  Školjka
Školjka 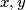 and
and  in positive integer:
in positive integer: 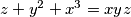 and
and 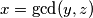 .
. 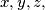 such that :
such that : 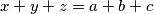
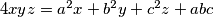
 touches the sides
touches the sides  ,
,  respectively.
respectively.  is a point inside triangle of
is a point inside triangle of  touches
touches  , and touches
, and touches 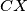 and
and 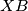 at
at  and
and  respectively.
respectively. 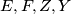 are concyclic.
are concyclic. 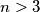 for which there exist
for which there exist  points
points 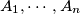 in the plane, no three collinear, and real numbers
in the plane, no three collinear, and real numbers 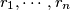 such that for
such that for 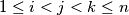 , the area of
, the area of 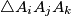 is
is 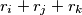 .
. 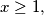 let
let 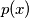 be the least prime that does not divide
be the least prime that does not divide 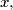 and define
and define 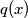 to be the product of all primes less than
to be the product of all primes less than 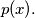 In particular,
In particular, 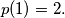 For
For  having
having 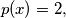 define
define 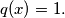 Consider the sequence
Consider the sequence 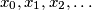 defined by
defined by 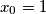 and
and 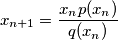 for
for 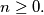 Find all
Find all 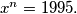
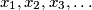 are positive real numbers for which
are positive real numbers for which 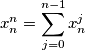 for
for 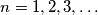 Prove that
Prove that