Does there exist an integer
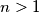
which satisfies the following condition? The set of positive integers can be partitioned into

nonempty subsets, such that an arbitrary sum of
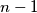
integers, one taken from each of any
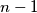
of the subsets, lies in the remaining subset.
%V0
Does there exist an integer $n > 1$ which satisfies the following condition? The set of positive integers can be partitioned into $n$ nonempty subsets, such that an arbitrary sum of $n - 1$ integers, one taken from each of any $n - 1$ of the subsets, lies in the remaining subset.