Find the maximum value of
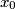
for which there exists a sequence
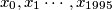
of positive reals with
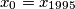
, such that
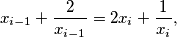
for all
.
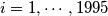
%V0
Find the maximum value of $x_{0}$ for which there exists a sequence $x_{0},x_{1}\cdots ,x_{1995}$ of positive reals with $x_{0} = x_{1995}$, such that
$$x_{i - 1} + \frac {2}{x_{i - 1}} = 2x_{i} + \frac {1}{x_{i}},$$
for all $i = 1,\cdots ,1995$.
Školjka