Let
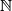
denote the set of all positive integers. Prove that there exists a unique function
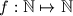
satisfying
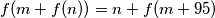
for all

and

in
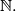
What is the value of
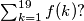
%V0
Let $\mathbb{N}$ denote the set of all positive integers. Prove that there exists a unique function $f: \mathbb{N} \mapsto \mathbb{N}$ satisfying
$$f(m + f(n)) = n + f(m + 95)$$
for all $m$ and $n$ in $\mathbb{N}.$ What is the value of $\sum^{19}_{k = 1} f(k)?$