Let
be integers such that
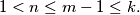
Determine the maximum size of a subset
of the set
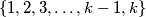
such that no
distinct elements of
add up to
%V0
Let $k,m,n$ be integers such that $1 < n \leq m - 1 \leq k.$ Determine the maximum size of a subset $S$ of the set $\{1,2,3, \ldots, k-1,k\}$ such that no $n$ distinct elements of $S$ add up to $m.$
Školjka