let

be a finitive set and

and

be two injective surjective functions from

to

.let

and

be two sets such that they are defined as following
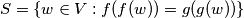
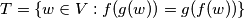
we know that
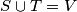
, prove:
for each
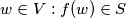
if and only if
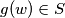
%V0
let $V$ be a finitive set and $g$ and $f$ be two injective surjective functions from $V$to$V$.let $T$ and $S$ be two sets such that they are defined as following
$S = \{w \in V: f(f(w)) = g(g(w))\}$
$T = \{w \in V: f(g(w)) = g(f(w))\}$
we know that $S \cup T = V$, prove:
for each $w \in V : f(w) \in S$ if and only if $g(w) \in S$