IMO Shortlist 1999 problem A6
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0 For  and
and 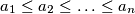 given real numbers we have the following instructions:
given real numbers we have the following instructions:
- place out the numbers in some order in a ring;
- delete one of the numbers from the ring;
- if just two numbers are remaining in the ring: let be the sum of these two numbers. Otherwise, if there are more the two numbers in the ring, replace
be the sum of these two numbers. Otherwise, if there are more the two numbers in the ring, replace
Afterwards start again with the step (2). Show that the largest sum which can result in this way is given by the formula
which can result in this way is given by the formula
![S_{max}= \sum^n_{k=2} \begin{pmatrix} n -2 \\ [\frac{k}{2}] - 1\end{pmatrix}a_{k}.](/media/m/a/d/4/ad4e65bc42b08da06d18502a103d6a04.png)
 and
and 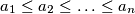 given real numbers we have the following instructions:
given real numbers we have the following instructions: - place out the numbers in some order in a ring;
- delete one of the numbers from the ring;
- if just two numbers are remaining in the ring: let
 be the sum of these two numbers. Otherwise, if there are more the two numbers in the ring, replace
be the sum of these two numbers. Otherwise, if there are more the two numbers in the ring, replace Afterwards start again with the step (2). Show that the largest sum
 which can result in this way is given by the formula
which can result in this way is given by the formula ![S_{max}= \sum^n_{k=2} \begin{pmatrix} n -2 \\ [\frac{k}{2}] - 1\end{pmatrix}a_{k}.](/media/m/a/d/4/ad4e65bc42b08da06d18502a103d6a04.png)
Izvor: Međunarodna matematička olimpijada, shortlist 1999
 Školjka
Školjka 
