Let
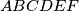
be a convex hexagon such that

is parallel to
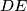
,

is parallel to

, and

is parallel to
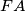
. Let
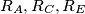
denote the circumradii of triangles
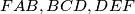
, respectively, and let

denote the perimeter of the hexagon. Prove that
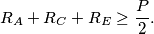
%V0
Let $ABCDEF$ be a convex hexagon such that $AB$ is parallel to $DE$, $BC$ is parallel to $EF$, and $CD$ is parallel to $FA$. Let $R_{A},R_{C},R_{E}$ denote the circumradii of triangles $FAB,BCD,DEF$, respectively, and let $P$ denote the perimeter of the hexagon. Prove that
$$R_{A} + R_{C} + R_{E}\geq \frac {P}{2}.$$