Let
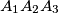
be a non-isosceles triangle with incenter
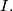
Let
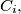
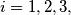
be the smaller circle through

tangent to
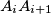
and
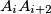
(the addition of indices being mod 3). Let
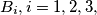
be the second point of intersection of
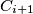
and
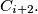
Prove that the circumcentres of the triangles
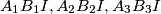
are collinear.
%V0
Let $A_1A_2A_3$ be a non-isosceles triangle with incenter $I.$ Let $C_i,$ $i = 1, 2, 3,$ be the smaller circle through $I$ tangent to $A_iA_{i+1}$ and $A_iA_{i+2}$ (the addition of indices being mod 3). Let $B_i, i = 1, 2, 3,$ be the second point of intersection of $C_{i+1}$ and $C_{i+2}.$ Prove that the circumcentres of the triangles $A_1 B_1I,A_2B_2I,A_3B_3I$ are collinear.