Let
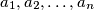
be positive real numbers such that
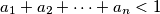
. Prove that
![\frac{a_{1} a_{2} \cdots a_{n} \left[ 1 - (a_{1} + a_{2} + \cdots + a_{n}) \right] }{(a_{1} + a_{2} + \cdots + a_{n})( 1 - a_1)(1 - a_2) \cdots (1 - a_n)} \leqslant \frac{1}{n^{n+1}}](/media/m/0/b/a/0bab773e1ec6962f3cabbe1b3882b9ff.png)
%V0
Let $a_{1},a_{2},\ldots ,a_{n}$ be positive real numbers such that $a_{1}+a_{2}+\cdots +a_{n}<1$. Prove that
$$\frac{a_{1} a_{2} \cdots a_{n} \left[ 1 - (a_{1} + a_{2} + \cdots + a_{n}) \right] }{(a_{1} + a_{2} + \cdots + a_{n})( 1 - a_1)(1 - a_2) \cdots (1 - a_n)} \leqslant \frac{1}{n^{n+1}}$$
Školjka