For any two nonnegative integers
and
satisfying
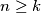
, we define the number
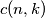
as follows:
-
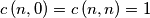
for all
;
-
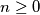
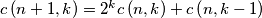
for
.
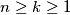
Prove that
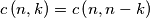
for all
.
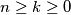
%V0
For any two nonnegative integers $n$ and $k$ satisfying $n\geq k$, we define the number $c(n,k)$ as follows:
- $c\left(n,0\right)=c\left(n,n\right)=1$ for all $n\geq 0$;
- $c\left(n+1,k\right)=2^{k}c\left(n,k\right)+c\left(n,k-1\right)$ for $n\geq k\geq 1$.
Prove that $c\left(n,k\right)=c\left(n,n-k\right)$ for all $n\geq k\geq 0$.
Školjka