Determine the least possible value of
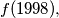
where
is a function from the set
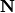
of positive integers into itself such that for all
,
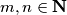
![f\left( n^{2}f(m)\right) =m\left[ f(n)\right] ^{2}.](/media/m/d/0/d/d0d1f5a0ff4ad4cf2a895d94af1a10b4.png)
%V0
Determine the least possible value of $f(1998),$ where $f$ is a function from the set ${\bf N}$ of positive integers into itself such that for all $m,n\in {\bf N}$,
$$f\left( n^{2}f(m)\right) =m\left[ f(n)\right] ^{2}.$$
Školjka