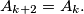Let 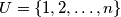 , where
, where 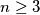 . A subset
. A subset  of
of  is said to be split by an arrangement of the elements of
is said to be split by an arrangement of the elements of  if an element not in
if an element not in  occurs in the arrangement somewhere between two elements of
occurs in the arrangement somewhere between two elements of  . For example, 13542 splits
. For example, 13542 splits 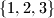 but not
but not 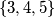 . Prove that for any
. Prove that for any  subsets of
subsets of  , each containing at least 2 and at most
, each containing at least 2 and at most 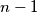 elements, there is an arrangement of the elements of
elements, there is an arrangement of the elements of  which splits all of them.
which splits all of them.
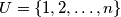 , where
, where 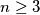 . A subset
. A subset  of
of  is said to be split by an arrangement of the elements of
is said to be split by an arrangement of the elements of  if an element not in
if an element not in  occurs in the arrangement somewhere between two elements of
occurs in the arrangement somewhere between two elements of  . For example, 13542 splits
. For example, 13542 splits 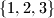 but not
but not 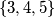 . Prove that for any
. Prove that for any  subsets of
subsets of  , each containing at least 2 and at most
, each containing at least 2 and at most 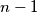 elements, there is an arrangement of the elements of
elements, there is an arrangement of the elements of  which splits all of them.
which splits all of them. Slični zadaci
Show that for any finite set  of distinct positive integers, we can find a set
of distinct positive integers, we can find a set  ⊇
⊇  such that every member of
such that every member of  divides the sum of all the members of
divides the sum of all the members of  .
.
Original Statement:
A finite set of (distinct) positive integers is called a DS-set if each of the integers divides the sum of them all. Prove that every finite set of positive integers is a subset of some DS-set.
 of distinct positive integers, we can find a set
of distinct positive integers, we can find a set  ⊇
⊇  such that every member of
such that every member of  divides the sum of all the members of
divides the sum of all the members of  .
. Original Statement:
A finite set of (distinct) positive integers is called a DS-set if each of the integers divides the sum of them all. Prove that every finite set of positive integers is a subset of some DS-set.
A rectangular array of numbers is given. In each row and each column, the sum of all numbers is an integer. Prove that each nonintegral number  in the array can be changed into either
in the array can be changed into either  or
or 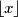 so that the row-sums and column-sums remain unchanged. (Note that
so that the row-sums and column-sums remain unchanged. (Note that  is the least integer greater than or equal to
is the least integer greater than or equal to  , while
, while 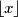 is the greatest integer less than or equal to
is the greatest integer less than or equal to  .)
.)
 in the array can be changed into either
in the array can be changed into either  or
or 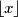 so that the row-sums and column-sums remain unchanged. (Note that
so that the row-sums and column-sums remain unchanged. (Note that  is the least integer greater than or equal to
is the least integer greater than or equal to  , while
, while 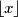 is the greatest integer less than or equal to
is the greatest integer less than or equal to  .)
.) Let  be an integer greater than 2. A positive integer is said to be attainable if it is 1 or can be obtained from 1 by a sequence of operations with the following properties:
be an integer greater than 2. A positive integer is said to be attainable if it is 1 or can be obtained from 1 by a sequence of operations with the following properties:
1.) The first operation is either addition or multiplication.
2.) Thereafter, additions and multiplications are used alternately.
3.) In each addition, one can choose independently whether to add 2 or
4.) In each multiplication, one can choose independently whether to multiply by 2 or by .
.
A positive integer which cannot be so obtained is said to be unattainable.
a.) Prove that if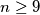 , there are infinitely many unattainable positive integers.
, there are infinitely many unattainable positive integers.
b.) Prove that if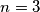 , all positive integers except 7 are attainable.
, all positive integers except 7 are attainable.
 be an integer greater than 2. A positive integer is said to be attainable if it is 1 or can be obtained from 1 by a sequence of operations with the following properties:
be an integer greater than 2. A positive integer is said to be attainable if it is 1 or can be obtained from 1 by a sequence of operations with the following properties: 1.) The first operation is either addition or multiplication.
2.) Thereafter, additions and multiplications are used alternately.
3.) In each addition, one can choose independently whether to add 2 or

4.) In each multiplication, one can choose independently whether to multiply by 2 or by
 .
. A positive integer which cannot be so obtained is said to be unattainable.
a.) Prove that if
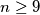 , there are infinitely many unattainable positive integers.
, there are infinitely many unattainable positive integers. b.) Prove that if
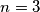 , all positive integers except 7 are attainable.
, all positive integers except 7 are attainable. Cards numbered 1 to 9 are arranged at random in a row. In a move, one may choose any block of consecutive cards whose numbers are in ascending or descending order, and switch the block around. For example, 9 1 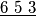
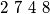 may be changed to
may be changed to 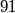
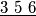
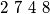 . Prove that in at most 12 moves, one can arrange the 9 cards so that their numbers are in ascending or descending order.
. Prove that in at most 12 moves, one can arrange the 9 cards so that their numbers are in ascending or descending order.
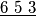
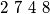 may be changed to
may be changed to 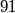
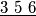
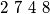 . Prove that in at most 12 moves, one can arrange the 9 cards so that their numbers are in ascending or descending order.
. Prove that in at most 12 moves, one can arrange the 9 cards so that their numbers are in ascending or descending order. Ten points are marked in the plane so that no three of them lie on a line. Each pair of points is connected with a segment. Each of these segments is painted with one of  colors, in such a way that for any
colors, in such a way that for any  of the ten points, there are
of the ten points, there are  segments each joining two of them and no two being painted with the same color. Determine all integers
segments each joining two of them and no two being painted with the same color. Determine all integers  ,
, 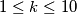 , for which this is possible.
, for which this is possible.
 colors, in such a way that for any
colors, in such a way that for any  of the ten points, there are
of the ten points, there are  segments each joining two of them and no two being painted with the same color. Determine all integers
segments each joining two of them and no two being painted with the same color. Determine all integers  ,
, 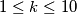 , for which this is possible.
, for which this is possible.  Školjka
Školjka  and
and 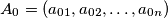 be any
be any 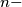 tuple of natural numbers, such that
tuple of natural numbers, such that 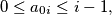 for
for 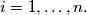
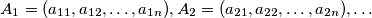 are defined by:
are defined by: 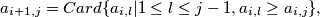 for
for 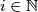 and
and 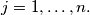 Prove that there exists
Prove that there exists 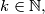 such that
such that