A solitaire game is played on an 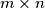 rectangular board, using
rectangular board, using  markers which are white on one side and black on the other. Initially, each square of the board contains a marker with its white side up, except for one corner square, which contains a marker with its black side up. In each move, one may take away one marker with its black side up, but must then turn over all markers which are in squares having an edge in common with the square of the removed marker. Determine all pairs
markers which are white on one side and black on the other. Initially, each square of the board contains a marker with its white side up, except for one corner square, which contains a marker with its black side up. In each move, one may take away one marker with its black side up, but must then turn over all markers which are in squares having an edge in common with the square of the removed marker. Determine all pairs 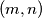 of positive integers such that all markers can be removed from the board.
of positive integers such that all markers can be removed from the board.
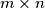 rectangular board, using
rectangular board, using  markers which are white on one side and black on the other. Initially, each square of the board contains a marker with its white side up, except for one corner square, which contains a marker with its black side up. In each move, one may take away one marker with its black side up, but must then turn over all markers which are in squares having an edge in common with the square of the removed marker. Determine all pairs
markers which are white on one side and black on the other. Initially, each square of the board contains a marker with its white side up, except for one corner square, which contains a marker with its black side up. In each move, one may take away one marker with its black side up, but must then turn over all markers which are in squares having an edge in common with the square of the removed marker. Determine all pairs 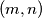 of positive integers such that all markers can be removed from the board.
of positive integers such that all markers can be removed from the board. Slični zadaci
Ten points are marked in the plane so that no three of them lie on a line. Each pair of points is connected with a segment. Each of these segments is painted with one of  colors, in such a way that for any
colors, in such a way that for any  of the ten points, there are
of the ten points, there are  segments each joining two of them and no two being painted with the same color. Determine all integers
segments each joining two of them and no two being painted with the same color. Determine all integers  ,
, 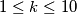 , for which this is possible.
, for which this is possible.
 colors, in such a way that for any
colors, in such a way that for any  of the ten points, there are
of the ten points, there are  segments each joining two of them and no two being painted with the same color. Determine all integers
segments each joining two of them and no two being painted with the same color. Determine all integers  ,
, 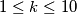 , for which this is possible.
, for which this is possible. Let 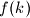 be the number of all non-negative integers
be the number of all non-negative integers  satisfying the following conditions:
satisfying the following conditions:
(1) The integer has exactly
has exactly  digits in the decimal representation (where the first digit is not necessarily non-zero!), i. e. we have
digits in the decimal representation (where the first digit is not necessarily non-zero!), i. e. we have 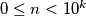 .
.
(2) These digits of n can be permuted in such a way that the resulting number is divisible by 11.
digits of n can be permuted in such a way that the resulting number is divisible by 11.
Show that for any positive integer number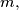 we have
we have 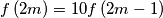 .
.
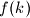 be the number of all non-negative integers
be the number of all non-negative integers  satisfying the following conditions:
satisfying the following conditions: (1) The integer
 has exactly
has exactly  digits in the decimal representation (where the first digit is not necessarily non-zero!), i. e. we have
digits in the decimal representation (where the first digit is not necessarily non-zero!), i. e. we have 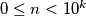 .
. (2) These
 digits of n can be permuted in such a way that the resulting number is divisible by 11.
digits of n can be permuted in such a way that the resulting number is divisible by 11. Show that for any positive integer number
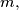 we have
we have 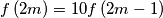 .
.  Školjka
Školjka 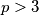 be a prime number. For each nonempty subset
be a prime number. For each nonempty subset  of
of 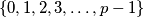 , let
, let 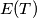 be the set of all
be the set of all 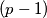 -tuples
-tuples 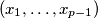 , where each
, where each 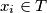 and
and 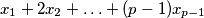 is divisible by
is divisible by  and let
and let 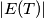 denote the number of elements in
denote the number of elements in 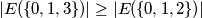
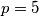 .
.  ,
, 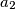 ,
,  ,
,  are integers such that
are integers such that 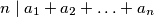 .
. 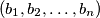 and
and 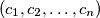 of
of 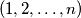 such that for each integer
such that for each integer  with
with 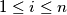 , we have
, we have 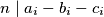
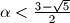 be a positive real number. Prove that there exist positive integers
be a positive real number. Prove that there exist positive integers 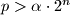 for which one can select
for which one can select 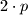 pairwise distinct subsets
pairwise distinct subsets 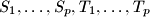 of the set
of the set 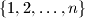 such that
such that 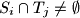 for all
for all 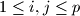
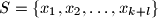 be a
be a 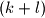 -element set of real numbers contained in the interval
-element set of real numbers contained in the interval ![[0, 1]](/media/m/7/f/0/7f04c41d91b0555ac792351e836cbd4e.png) ;
;  are positive integers. A
are positive integers. A 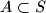 is called nice if
is called nice if 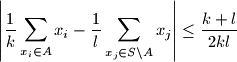
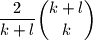 .
.