Let

be the incenter of triangle

. Let
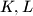
and

be the points of tangency of the incircle of

with
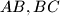
and

, respectively. The line

passes through

and is parallel to
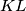
. The lines
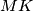
and
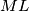
intersect

at the points

and

. Prove that
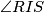
is acute.
%V0
Let $I$ be the incenter of triangle $ABC$. Let $K,L$ and $M$ be the points of tangency of the incircle of $ABC$ with $AB,BC$ and $CA$, respectively. The line $t$ passes through $B$ and is parallel to $KL$. The lines $MK$ and $ML$ intersect $t$ at the points $R$ and $S$. Prove that $\angle RIS$ is acute.