IMO Shortlist 2002 problem G3
Dodao/la:
arhiva2. travnja 2012. The circle

has centre
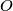
, and

is a diameter of

. Let

be a point of

such that
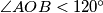
. Let

be the midpoint of the arc

which does not contain

. The line through
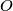
parallel to

meets the line

at

. The perpendicular bisector of
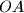
meets

at

and at

. Prove that

is the incentre of the triangle
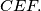
%V0
The circle $S$ has centre $O$, and $BC$ is a diameter of $S$. Let $A$ be a point of $S$ such that $\angle AOB<120{{}^\circ}$. Let $D$ be the midpoint of the arc $AB$ which does not contain $C$. The line through $O$ parallel to $DA$ meets the line $AC$ at $I$. The perpendicular bisector of $OA$ meets $S$ at $E$ and at $F$. Prove that $I$ is the incentre of the triangle $CEF.$
Izvor: Međunarodna matematička olimpijada, shortlist 2002