Slični zadaci
Let  be a triangle such that
be a triangle such that 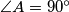 and
and 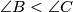 . The tangent at
. The tangent at  to the circumcircle
to the circumcircle  of triangle
of triangle  meets the line
meets the line  at
at  . Let
. Let  be the reflection of
be the reflection of  in the line
in the line  , let
, let  be the foot of the perpendicular from
be the foot of the perpendicular from  to
to  , and let
, and let  be the midpoint of the segment
be the midpoint of the segment 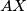 . Let the line
. Let the line 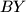 intersect the circle
intersect the circle  again at
again at  .
.
Prove that the line is tangent to the circumcircle of triangle
is tangent to the circumcircle of triangle 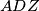 .
.
commentEdited by Orl.
 be a triangle such that
be a triangle such that 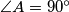 and
and 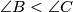 . The tangent at
. The tangent at  to the circumcircle
to the circumcircle  of triangle
of triangle  meets the line
meets the line  at
at  . Let
. Let  be the reflection of
be the reflection of  in the line
in the line  , let
, let  be the foot of the perpendicular from
be the foot of the perpendicular from  to
to  , and let
, and let  be the midpoint of the segment
be the midpoint of the segment 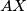 . Let the line
. Let the line 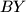 intersect the circle
intersect the circle  again at
again at  .
. Prove that the line
 is tangent to the circumcircle of triangle
is tangent to the circumcircle of triangle 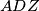 .
. commentEdited by Orl.
Point  lies on side
lies on side  of a convex quadrilateral
of a convex quadrilateral  . Let
. Let  be the incircle of triangle
be the incircle of triangle 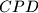 , and let
, and let  be its incenter. Suppose that
be its incenter. Suppose that  is tangent to the incircles of triangles
is tangent to the incircles of triangles 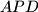 and
and 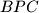 at points
at points  and
and  , respectively. Let lines
, respectively. Let lines  and
and  meet at
meet at  , and let lines
, and let lines 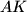 and
and 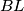 meet at
meet at  . Prove that points
. Prove that points  ,
,  , and
, and  are collinear.
are collinear.
Author: Waldemar Pompe, Poland
 lies on side
lies on side  of a convex quadrilateral
of a convex quadrilateral  . Let
. Let  be the incircle of triangle
be the incircle of triangle 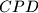 , and let
, and let  be its incenter. Suppose that
be its incenter. Suppose that  is tangent to the incircles of triangles
is tangent to the incircles of triangles 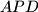 and
and 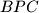 at points
at points  and
and  , respectively. Let lines
, respectively. Let lines  and
and  meet at
meet at  , and let lines
, and let lines 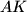 and
and 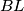 meet at
meet at  . Prove that points
. Prove that points  ,
,  , and
, and  are collinear.
are collinear. Author: Waldemar Pompe, Poland
 Školjka
Školjka 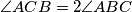 . Let
. Let 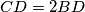 . The segment
. The segment  is extended to
is extended to 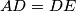 . Prove that
. Prove that 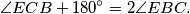
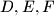 of an equilateral triangle lie on the sides
of an equilateral triangle lie on the sides 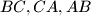 respectively of a triangle
respectively of a triangle  If
If  are the respective lengths of these sides, and
are the respective lengths of these sides, and  the area of
the area of 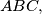 prove that
prove that 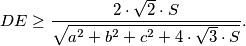
 its orthocenter,
its orthocenter,  its circumcenter, and
its circumcenter, and  its circumradius. Let
its circumradius. Let  across the line
across the line  , and let
, and let  across the line
across the line 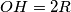 .
. 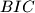 ,
, 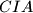 and
and 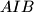 , respectively. Let the triangle
, respectively. Let the triangle 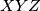 be equilateral. Prove that
be equilateral. Prove that  be a line through
be a line through  and the line
and the line  in
in  . Denote by
. Denote by 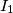 ,
, 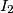 and
and 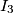 the incenters of
the incenters of 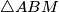 ,
, 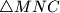 and
and 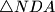 , respectively. Prove that the orthocenter of
, respectively. Prove that the orthocenter of 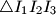 lies on
lies on