Let  be a triangle such that
be a triangle such that 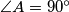 and
and 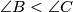 . The tangent at
. The tangent at  to the circumcircle
to the circumcircle  of triangle
of triangle  meets the line
meets the line  at
at  . Let
. Let  be the reflection of
be the reflection of  in the line
in the line  , let
, let  be the foot of the perpendicular from
be the foot of the perpendicular from  to
to  , and let
, and let  be the midpoint of the segment
be the midpoint of the segment 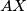 . Let the line
. Let the line 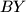 intersect the circle
intersect the circle  again at
again at  .
.
Prove that the line is tangent to the circumcircle of triangle
is tangent to the circumcircle of triangle 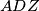 .
.
commentEdited by Orl.
 be a triangle such that
be a triangle such that 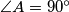 and
and 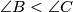 . The tangent at
. The tangent at  to the circumcircle
to the circumcircle  of triangle
of triangle  meets the line
meets the line  at
at  . Let
. Let  be the reflection of
be the reflection of  in the line
in the line  , let
, let  be the foot of the perpendicular from
be the foot of the perpendicular from  to
to  , and let
, and let  be the midpoint of the segment
be the midpoint of the segment 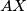 . Let the line
. Let the line 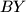 intersect the circle
intersect the circle  again at
again at  .
. Prove that the line
 is tangent to the circumcircle of triangle
is tangent to the circumcircle of triangle 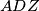 .
. commentEdited by Orl.
 Školjka
Školjka