IMO Shortlist 2006 problem G7
Kvaliteta:
Avg: 0,0Težina:
Avg: 9,0 In a triangle  , let
, let 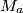 ,
, 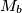 ,
, 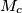 be the midpoints of the sides
be the midpoints of the sides  ,
,  ,
,  , respectively, and
, respectively, and 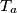 ,
, 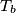 ,
, 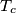 be the midpoints of the arcs
be the midpoints of the arcs  ,
,  ,
,  of the circumcircle of
of the circumcircle of  , not containing the vertices
, not containing the vertices  ,
,  ,
,  , respectively. For
, respectively. For 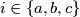 , let
, let 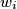 be the circle with
be the circle with 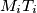 as diameter. Let
as diameter. Let 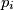 be the common external common tangent to the circles
be the common external common tangent to the circles 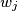 and
and 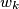 (for all
(for all 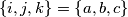 ) such that
) such that 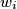 lies on the opposite side of
lies on the opposite side of 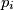 than
than 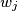 and
and 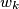 do.
do.
Prove that the lines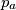 ,
, 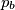 ,
, 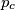 form a triangle similar to
form a triangle similar to  and find the ratio of similitude.
and find the ratio of similitude.
 , let
, let 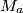 ,
, 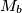 ,
, 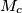 be the midpoints of the sides
be the midpoints of the sides  ,
,  ,
,  , respectively, and
, respectively, and 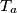 ,
, 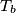 ,
, 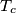 be the midpoints of the arcs
be the midpoints of the arcs  ,
,  ,
,  of the circumcircle of
of the circumcircle of  , not containing the vertices
, not containing the vertices  ,
,  ,
,  , respectively. For
, respectively. For 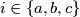 , let
, let 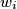 be the circle with
be the circle with 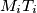 as diameter. Let
as diameter. Let 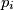 be the common external common tangent to the circles
be the common external common tangent to the circles 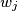 and
and 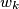 (for all
(for all 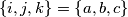 ) such that
) such that 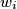 lies on the opposite side of
lies on the opposite side of 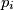 than
than 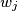 and
and 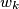 do.
do. Prove that the lines
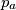 ,
, 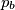 ,
, 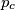 form a triangle similar to
form a triangle similar to  and find the ratio of similitude.
and find the ratio of similitude. Izvor: Međunarodna matematička olimpijada, shortlist 2006
 Školjka
Školjka 
