For any positive integer

, let
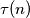
denote the number of its positive divisors (including 1 and itself). Determine all positive integers

for which there exists a positive integer

such that
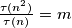
.
%V0
For any positive integer $n$, let $\tau (n)$ denote the number of its positive divisors (including 1 and itself). Determine all positive integers $m$ for which there exists a positive integer $n$ such that $\frac{\tau (n^{2})}{\tau (n)}=m$.