IMO Shortlist 2007 problem N6
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0 Let  be a positive integer. Prove that the number
be a positive integer. Prove that the number 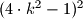 has a positive divisor of the form
has a positive divisor of the form 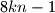 if and only if
if and only if  is even.
is even.
Actual IMO 2007 Problem, posed as question 5 in the contest, which was used as a lemma in the official solutions for problem N6 as shown above.
Author: Kevin Buzzard and Edward Crane, United Kingdom
 be a positive integer. Prove that the number
be a positive integer. Prove that the number 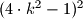 has a positive divisor of the form
has a positive divisor of the form 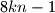 if and only if
if and only if  is even.
is even. Actual IMO 2007 Problem, posed as question 5 in the contest, which was used as a lemma in the official solutions for problem N6 as shown above.
Author: Kevin Buzzard and Edward Crane, United Kingdom
Izvor: Međunarodna matematička olimpijada, shortlist 2007
 Školjka
Školjka 
