Let

be a fixed integer. Find the least constant

such the inequality
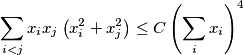
holds for any
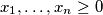
(the sum on the left consists of
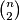
summands). For this constant

, characterize the instances of equality.
%V0
Let $n \geq 2$ be a fixed integer. Find the least constant $C$ such the inequality
$$\sum_{i<j} x_{i}x_{j} \left(x^{2}_{i}+x^{2}_{j} \right) \leq C \left(\sum_{i}x_{i} \right)^4$$
holds for any $x_{1}, \ldots ,x_{n} \geq 0$ (the sum on the left consists of $\binom{n}{2}$ summands). For this constant $C$, characterize the instances of equality.