Slični zadaci
Let two circles 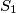 and
and 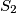 meet at the points
meet at the points  and
and  . A line through
. A line through  meets
meets 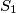 again at
again at  and
and 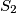 again at
again at  . Let
. Let  ,
,  ,
,  be three points on the line segments
be three points on the line segments  ,
,  ,
,  respectively, with
respectively, with  parallel to
parallel to  and
and 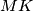 parallel to
parallel to  . Let
. Let  and
and  be points on those arcs
be points on those arcs  of
of 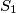 and
and  of
of 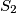 respectively that do not contain
respectively that do not contain  . Given that
. Given that 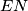 is perpendicular to
is perpendicular to  and
and 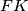 is perpendicular to
is perpendicular to  prove that
prove that 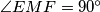 .
.
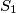 and
and 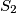 meet at the points
meet at the points  and
and  . A line through
. A line through  meets
meets 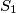 again at
again at  and
and 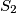 again at
again at  . Let
. Let  ,
,  ,
,  be three points on the line segments
be three points on the line segments  ,
,  ,
,  respectively, with
respectively, with  parallel to
parallel to  and
and 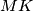 parallel to
parallel to  . Let
. Let  and
and  be points on those arcs
be points on those arcs  of
of 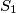 and
and  of
of 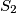 respectively that do not contain
respectively that do not contain  . Given that
. Given that 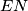 is perpendicular to
is perpendicular to  and
and 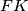 is perpendicular to
is perpendicular to  prove that
prove that 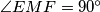 .
. Suppose we have a  -gon. Some
-gon. Some 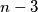 diagonals are coloured black and some other
diagonals are coloured black and some other 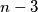 diagonals are coloured red (a side is not a diagonal), so that no two diagonals of the same colour can intersect strictly inside the polygon, although they can share a vertex. Find the maximum number of intersection points between diagonals coloured differently strictly inside the polygon, in terms of
diagonals are coloured red (a side is not a diagonal), so that no two diagonals of the same colour can intersect strictly inside the polygon, although they can share a vertex. Find the maximum number of intersection points between diagonals coloured differently strictly inside the polygon, in terms of  .
.
 -gon. Some
-gon. Some 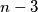 diagonals are coloured black and some other
diagonals are coloured black and some other 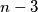 diagonals are coloured red (a side is not a diagonal), so that no two diagonals of the same colour can intersect strictly inside the polygon, although they can share a vertex. Find the maximum number of intersection points between diagonals coloured differently strictly inside the polygon, in terms of
diagonals are coloured red (a side is not a diagonal), so that no two diagonals of the same colour can intersect strictly inside the polygon, although they can share a vertex. Find the maximum number of intersection points between diagonals coloured differently strictly inside the polygon, in terms of  .
. Consider a convex polyhaedron without parallel edges and without an edge parallel to any face other than the two faces adjacent to it. Call a pair of points of the polyhaedron antipodal if there exist two parallel planes passing through these points and such that the polyhaedron is contained between these planes. Let  be the number of antipodal pairs of vertices, and let
be the number of antipodal pairs of vertices, and let  be the number of antipodal pairs of midpoint edges. Determine the difference
be the number of antipodal pairs of midpoint edges. Determine the difference 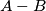 in terms of the numbers of vertices, edges, and faces.
in terms of the numbers of vertices, edges, and faces.
 be the number of antipodal pairs of vertices, and let
be the number of antipodal pairs of vertices, and let  be the number of antipodal pairs of midpoint edges. Determine the difference
be the number of antipodal pairs of midpoint edges. Determine the difference 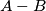 in terms of the numbers of vertices, edges, and faces.
in terms of the numbers of vertices, edges, and faces.  Školjka
Školjka  , such that
, such that 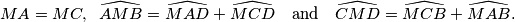
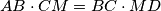 and
and 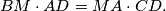
 . The points
. The points  of the triangle
of the triangle  ,
,  . Let
. Let  be a variable point on the arc
be a variable point on the arc 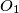 and
and 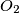 be the incenters of the triangles
be the incenters of the triangles 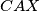 and
and 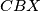 . Prove that the circumcircle of the triangle
. Prove that the circumcircle of the triangle 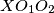 intersects the circle
intersects the circle  inside the quadrilateral. Suppose that
inside the quadrilateral. Suppose that 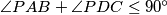 and
and 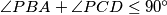 .
. 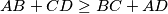 .
.