Slični zadaci
A circle  bisects a circle
bisects a circle  if it cuts
if it cuts  at opposite ends of a diameter.
at opposite ends of a diameter.  ,
,  ,
, are circles with distinct centers
are circles with distinct centers  (respectively).
(respectively).
Show that are collinear iff there is no unique circle
are collinear iff there is no unique circle  which bisects each of
which bisects each of  ,
,  ,
, . Show that if there is more than one circle
. Show that if there is more than one circle  which bisects each of
which bisects each of  ,
,  ,
, , then all such circles pass through two fixed points. Find these points.
, then all such circles pass through two fixed points. Find these points.
Original Statement:
A circle is said to cut a circle
is said to cut a circle 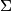 diametrically if and only if their common chord is a diameter of
diametrically if and only if their common chord is a diameter of 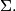
Let be three circles with distinct centres
be three circles with distinct centres  respectively. Prove that
respectively. Prove that  are collinear if and only if there is no unique circle
are collinear if and only if there is no unique circle  which cuts each of
which cuts each of  diametrically. Prove further that if there exists more than one circle
diametrically. Prove further that if there exists more than one circle  which cuts each
which cuts each  diametrically, then all such circles
diametrically, then all such circles  pass through two fixed points. Locate these points in relation to the circles
pass through two fixed points. Locate these points in relation to the circles 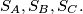
 bisects a circle
bisects a circle  if it cuts
if it cuts  at opposite ends of a diameter.
at opposite ends of a diameter.  ,
,  ,
, are circles with distinct centers
are circles with distinct centers  (respectively).
(respectively). Show that
 are collinear iff there is no unique circle
are collinear iff there is no unique circle  which bisects each of
which bisects each of  ,
,  ,
, . Show that if there is more than one circle
. Show that if there is more than one circle  which bisects each of
which bisects each of  ,
,  ,
, , then all such circles pass through two fixed points. Find these points.
, then all such circles pass through two fixed points. Find these points. Original Statement:
A circle
 is said to cut a circle
is said to cut a circle 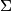 diametrically if and only if their common chord is a diameter of
diametrically if and only if their common chord is a diameter of 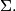
Let
 be three circles with distinct centres
be three circles with distinct centres  respectively. Prove that
respectively. Prove that  are collinear if and only if there is no unique circle
are collinear if and only if there is no unique circle  which cuts each of
which cuts each of  diametrically. Prove further that if there exists more than one circle
diametrically. Prove further that if there exists more than one circle  which cuts each
which cuts each  diametrically, then all such circles
diametrically, then all such circles  pass through two fixed points. Locate these points in relation to the circles
pass through two fixed points. Locate these points in relation to the circles 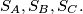
Let 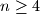 be a fixed positive integer. Given a set
be a fixed positive integer. Given a set 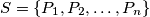 of
of  points in the plane such that no three are collinear and no four concyclic, let
points in the plane such that no three are collinear and no four concyclic, let 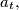
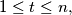 be the number of circles
be the number of circles 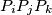 that contain
that contain 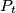 in their interior, and let
in their interior, and let 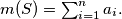 Prove that there exists a positive integer
Prove that there exists a positive integer 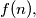 depending only on
depending only on 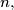 such that the points of
such that the points of  are the vertices of a convex polygon if and only if
are the vertices of a convex polygon if and only if 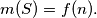
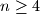 be a fixed positive integer. Given a set
be a fixed positive integer. Given a set 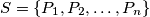 of
of  points in the plane such that no three are collinear and no four concyclic, let
points in the plane such that no three are collinear and no four concyclic, let 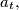
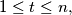 be the number of circles
be the number of circles 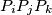 that contain
that contain 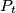 in their interior, and let
in their interior, and let 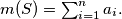 Prove that there exists a positive integer
Prove that there exists a positive integer 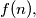 depending only on
depending only on 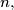 such that the points of
such that the points of  are the vertices of a convex polygon if and only if
are the vertices of a convex polygon if and only if 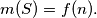
Given three fixed pairwisely distinct points  ,
,  ,
,  lying on one straight line in this order. Let
lying on one straight line in this order. Let  be a circle passing through
be a circle passing through  and
and  whose center does not lie on the line
whose center does not lie on the line  . The tangents to
. The tangents to  at
at  and
and  intersect each other at a point
intersect each other at a point  . The segment
. The segment 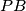 meets the circle
meets the circle  at
at  .
.
Show that the point of intersection of the angle bisector of the angle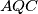 with the line
with the line  does not depend on the choice of the circle
does not depend on the choice of the circle  .
.
 ,
,  ,
,  lying on one straight line in this order. Let
lying on one straight line in this order. Let  be a circle passing through
be a circle passing through  and
and  whose center does not lie on the line
whose center does not lie on the line  . The tangents to
. The tangents to  at
at  and
and  intersect each other at a point
intersect each other at a point  . The segment
. The segment 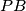 meets the circle
meets the circle  at
at  .
. Show that the point of intersection of the angle bisector of the angle
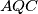 with the line
with the line  does not depend on the choice of the circle
does not depend on the choice of the circle  .
. Let 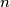 and
and  be positive integers. There are given
be positive integers. There are given 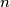 circles in the plane. Every two of them intersect at two distinct points, and all points of intersection they determine are pairwisely distinct (i. e. no three circles have a common point). No three circles have a point in common. Each intersection point must be colored with one of
circles in the plane. Every two of them intersect at two distinct points, and all points of intersection they determine are pairwisely distinct (i. e. no three circles have a common point). No three circles have a point in common. Each intersection point must be colored with one of  distinct colors so that each color is used at least once and exactly
distinct colors so that each color is used at least once and exactly  distinct colors occur on each circle. Find all values of
distinct colors occur on each circle. Find all values of 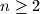 and
and  for which such a coloring is possible.
for which such a coloring is possible.
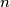 and
and  be positive integers. There are given
be positive integers. There are given 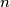 circles in the plane. Every two of them intersect at two distinct points, and all points of intersection they determine are pairwisely distinct (i. e. no three circles have a common point). No three circles have a point in common. Each intersection point must be colored with one of
circles in the plane. Every two of them intersect at two distinct points, and all points of intersection they determine are pairwisely distinct (i. e. no three circles have a common point). No three circles have a point in common. Each intersection point must be colored with one of  distinct colors so that each color is used at least once and exactly
distinct colors so that each color is used at least once and exactly  distinct colors occur on each circle. Find all values of
distinct colors occur on each circle. Find all values of 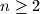 and
and  for which such a coloring is possible.
for which such a coloring is possible. Let  be a circle and let
be a circle and let  be a line such that
be a line such that  and
and  have no common points. Further, let
have no common points. Further, let  be a diameter of the circle
be a diameter of the circle  ; assume that this diameter
; assume that this diameter  is perpendicular to the line
is perpendicular to the line  , and the point
, and the point  is nearer to the line
is nearer to the line  than the point
than the point  . Let
. Let  be an arbitrary point on the circle
be an arbitrary point on the circle  , different from the points
, different from the points  and
and  . Let
. Let  be the point of intersection of the lines
be the point of intersection of the lines  and
and  . One of the two tangents from the point
. One of the two tangents from the point  to the circle
to the circle  touches this circle
touches this circle  at a point
at a point  ; hereby, we assume that the points
; hereby, we assume that the points  and
and  lie in the same halfplane with respect to the line
lie in the same halfplane with respect to the line  . Denote by
. Denote by  the point of intersection of the lines
the point of intersection of the lines  and
and  . Let the line
. Let the line 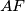 intersect the circle
intersect the circle  at a point
at a point  , different from
, different from  .
.
Prove that the reflection of the point in the line
in the line  lies on the line
lies on the line 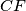 .
.
 be a circle and let
be a circle and let  be a line such that
be a line such that  and
and  have no common points. Further, let
have no common points. Further, let  be a diameter of the circle
be a diameter of the circle  ; assume that this diameter
; assume that this diameter  is perpendicular to the line
is perpendicular to the line  , and the point
, and the point  is nearer to the line
is nearer to the line  than the point
than the point  . Let
. Let  be an arbitrary point on the circle
be an arbitrary point on the circle  , different from the points
, different from the points  and
and  . Let
. Let  be the point of intersection of the lines
be the point of intersection of the lines  and
and  . One of the two tangents from the point
. One of the two tangents from the point  to the circle
to the circle  touches this circle
touches this circle  at a point
at a point  ; hereby, we assume that the points
; hereby, we assume that the points  and
and  lie in the same halfplane with respect to the line
lie in the same halfplane with respect to the line  . Denote by
. Denote by  the point of intersection of the lines
the point of intersection of the lines  and
and  . Let the line
. Let the line 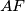 intersect the circle
intersect the circle  at a point
at a point  , different from
, different from  .
. Prove that the reflection of the point
 in the line
in the line  lies on the line
lies on the line 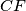 .
. Given trapezoid  with parallel sides
with parallel sides  and
and  , assume that there exist points
, assume that there exist points  on line
on line  outside segment
outside segment  , and
, and  inside segment
inside segment  such that
such that 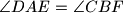 . Denote by
. Denote by  the point of intersection of
the point of intersection of  and
and  , and by
, and by 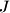 the point of intersection of
the point of intersection of  and
and  . Let
. Let  be the midpoint of segment
be the midpoint of segment  , assume it does not lie on line
, assume it does not lie on line  . Prove that
. Prove that  belongs to the circumcircle of
belongs to the circumcircle of 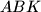 if and only if
if and only if  belongs to the circumcircle of
belongs to the circumcircle of 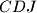 .
.
Proposed by Charles Leytem, Luxembourg
 with parallel sides
with parallel sides  and
and  , assume that there exist points
, assume that there exist points  on line
on line  outside segment
outside segment  , and
, and  inside segment
inside segment  such that
such that 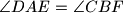 . Denote by
. Denote by  the point of intersection of
the point of intersection of  and
and  , and by
, and by 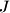 the point of intersection of
the point of intersection of  and
and  . Let
. Let  be the midpoint of segment
be the midpoint of segment  , assume it does not lie on line
, assume it does not lie on line  . Prove that
. Prove that  belongs to the circumcircle of
belongs to the circumcircle of 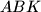 if and only if
if and only if  belongs to the circumcircle of
belongs to the circumcircle of 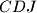 .
. Proposed by Charles Leytem, Luxembourg
 Školjka
Školjka  and
and  . Prove that there exist four points with the following property:
. Prove that there exist four points with the following property:  at
at  passes through one of these points.
passes through one of these points.