Slični zadaci
Let 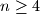 be a fixed positive integer. Given a set
be a fixed positive integer. Given a set 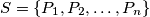 of
of  points in the plane such that no three are collinear and no four concyclic, let
points in the plane such that no three are collinear and no four concyclic, let 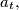
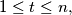 be the number of circles
be the number of circles 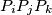 that contain
that contain 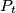 in their interior, and let
in their interior, and let 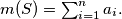 Prove that there exists a positive integer
Prove that there exists a positive integer 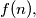 depending only on
depending only on 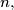 such that the points of
such that the points of  are the vertices of a convex polygon if and only if
are the vertices of a convex polygon if and only if 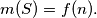
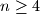 be a fixed positive integer. Given a set
be a fixed positive integer. Given a set 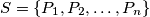 of
of  points in the plane such that no three are collinear and no four concyclic, let
points in the plane such that no three are collinear and no four concyclic, let 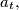
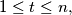 be the number of circles
be the number of circles 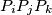 that contain
that contain 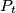 in their interior, and let
in their interior, and let 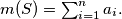 Prove that there exists a positive integer
Prove that there exists a positive integer 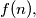 depending only on
depending only on 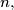 such that the points of
such that the points of  are the vertices of a convex polygon if and only if
are the vertices of a convex polygon if and only if 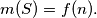
A number of  rectangles are drawn in the plane. Each rectangle has parallel sides and the sides of distinct rectangles lie on distinct lines. The rectangles divide the plane into a number of regions. For each region
rectangles are drawn in the plane. Each rectangle has parallel sides and the sides of distinct rectangles lie on distinct lines. The rectangles divide the plane into a number of regions. For each region  let
let 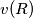 be the number of vertices. Take the sum
be the number of vertices. Take the sum 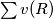 over the regions which have one or more vertices of the rectangles in their boundary. Show that this sum is less than
over the regions which have one or more vertices of the rectangles in their boundary. Show that this sum is less than 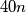 .
.
 rectangles are drawn in the plane. Each rectangle has parallel sides and the sides of distinct rectangles lie on distinct lines. The rectangles divide the plane into a number of regions. For each region
rectangles are drawn in the plane. Each rectangle has parallel sides and the sides of distinct rectangles lie on distinct lines. The rectangles divide the plane into a number of regions. For each region  let
let 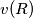 be the number of vertices. Take the sum
be the number of vertices. Take the sum 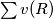 over the regions which have one or more vertices of the rectangles in their boundary. Show that this sum is less than
over the regions which have one or more vertices of the rectangles in their boundary. Show that this sum is less than 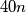 .
. Let  be an acute-angled triangle, and let
be an acute-angled triangle, and let  be the circumcircle of triangle
be the circumcircle of triangle  .
.
The tangent to the circle at the point
at the point  meets the tangent to the circle
meets the tangent to the circle  at
at  at the point
at the point 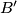 . The line
. The line 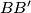 intersects the line
intersects the line  at
at  , and
, and  is the midpoint of the segment
is the midpoint of the segment  .
.
Similarly, the tangent to the circle at the point
at the point  meets the tangent to the circle
meets the tangent to the circle  at the point
at the point  at the point
at the point 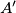 . The line
. The line 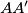 intersects the line
intersects the line  at
at  , and
, and  is the midpoint of the segment
is the midpoint of the segment  .
.
a) Show that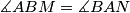 .
.
b) If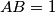 , determine the values of
, determine the values of  and
and  for the triangles
for the triangles  which maximise
which maximise 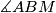 .
.
 be an acute-angled triangle, and let
be an acute-angled triangle, and let  be the circumcircle of triangle
be the circumcircle of triangle  .
. The tangent to the circle
 at the point
at the point  meets the tangent to the circle
meets the tangent to the circle  at
at  at the point
at the point 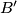 . The line
. The line 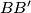 intersects the line
intersects the line  at
at  , and
, and  is the midpoint of the segment
is the midpoint of the segment  .
. Similarly, the tangent to the circle
 at the point
at the point  meets the tangent to the circle
meets the tangent to the circle  at the point
at the point  at the point
at the point 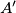 . The line
. The line 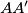 intersects the line
intersects the line  at
at  , and
, and  is the midpoint of the segment
is the midpoint of the segment  .
. a) Show that
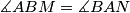 .
. b) If
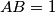 , determine the values of
, determine the values of  and
and  for the triangles
for the triangles  which maximise
which maximise 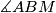 .
.  Školjka
Školjka  be a convex quadrilateral. The perpendicular bisectors of its sides
be a convex quadrilateral. The perpendicular bisectors of its sides  and
and  meet at
meet at  . Denote by
. Denote by  a point inside the quadrilateral
a point inside the quadrilateral 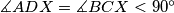 and
and 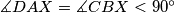 . Show that
. Show that 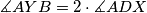 .
. 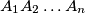 be a convex polygon,
be a convex polygon, 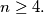 Prove that
Prove that 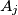 one can assign a pair
one can assign a pair 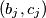 of real numbers,
of real numbers, 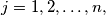 so that
so that 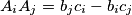 for all
for all 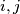 with
with 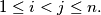
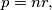 where
where  and
and  are respectively the semiperimeter and the inradius of a triangle with integer side lengths.
are respectively the semiperimeter and the inradius of a triangle with integer side lengths.