Neka su
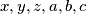
cijeli brojevi za koje vrijedi:
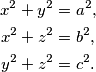
Dokažite da je broj
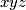
djeljiv s
,
.
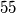
%V0
Neka su $x,y,z,a,b,c$ cijeli brojevi za koje vrijedi:$$$\begin{align*}
x^2+y^2&=a^2\text{,} \\
x^2+z^2&=b^2\text{,} \\
y^2+z^2&=c^2\text{.} \\
\end{align*}$$$ Dokažite da je broj $xyz$ djeljiv s
$(a)$ $5$,
$(b)$ $55$.
Školjka