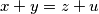
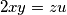
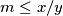
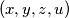
Consider the system , . Find the greatest value of the real constant such that for any positive integer solution of the system, with .
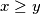
%V0
Consider the system $x + y = z + u$, $2xy = zu$. Find the greatest value of the real constant $m$ such that $m \leq x/y$ for any positive integer solution $(x,y,z,u)$ of the system, with $x \geq y$.
Izvor: Međunarodna matematička olimpijada, shortlist 2001
Školjka 
, 
. Find the greatest value of the real constant 
such that 
for any positive integer solution 
of the system, with 
.