Dokažite da za svaki realan broj
i svaki prirodan broj
vrijedi nejednakost
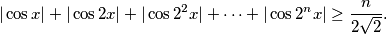
%V0
Dokažite da za svaki realan broj $x$ i svaki prirodan broj $n$ vrijedi nejednakost $$|\cos x| + |\cos 2x| + |\cos 2^2x| + \dots + |\cos 2^nx| \geq \frac{n}{2\sqrt{2}} \text{.}$$
Školjka