Twenty-one girls and twenty-one boys took part in a mathematical competition. It turned out that each contestant solved at most six problems, and for each pair of a girl and a boy, there was at least one problem that was solved by both the girl and the boy. Show that there is a problem that was solved by at least three girls and at least three boys.
Slični zadaci
A pile of  pebbles is placed in a vertical column. This configuration is modified according to the following rules. A pebble can be moved if it is at the top of a column which contains at least two more pebbles than the column immediately to its right. (If there are no pebbles to the right, think of this as a column with 0 pebbles.) At each stage, choose a pebble from among those that can be moved (if there are any) and place it at the top of the column to its right. If no pebbles can be moved, the configuration is called a final configuration. For each
pebbles is placed in a vertical column. This configuration is modified according to the following rules. A pebble can be moved if it is at the top of a column which contains at least two more pebbles than the column immediately to its right. (If there are no pebbles to the right, think of this as a column with 0 pebbles.) At each stage, choose a pebble from among those that can be moved (if there are any) and place it at the top of the column to its right. If no pebbles can be moved, the configuration is called a final configuration. For each  , show that, no matter what choices are made at each stage, the final configuration obtained is unique. Describe that configuration in terms of
, show that, no matter what choices are made at each stage, the final configuration obtained is unique. Describe that configuration in terms of  .
.
IMO ShortList 2001, combinatorics problem 7, alternative
 pebbles is placed in a vertical column. This configuration is modified according to the following rules. A pebble can be moved if it is at the top of a column which contains at least two more pebbles than the column immediately to its right. (If there are no pebbles to the right, think of this as a column with 0 pebbles.) At each stage, choose a pebble from among those that can be moved (if there are any) and place it at the top of the column to its right. If no pebbles can be moved, the configuration is called a final configuration. For each
pebbles is placed in a vertical column. This configuration is modified according to the following rules. A pebble can be moved if it is at the top of a column which contains at least two more pebbles than the column immediately to its right. (If there are no pebbles to the right, think of this as a column with 0 pebbles.) At each stage, choose a pebble from among those that can be moved (if there are any) and place it at the top of the column to its right. If no pebbles can be moved, the configuration is called a final configuration. For each  , show that, no matter what choices are made at each stage, the final configuration obtained is unique. Describe that configuration in terms of
, show that, no matter what choices are made at each stage, the final configuration obtained is unique. Describe that configuration in terms of  .
. IMO ShortList 2001, combinatorics problem 7, alternative
In a mathematical competition, in which 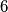 problems were posed to the participants, every two of these problems were solved by more than
problems were posed to the participants, every two of these problems were solved by more than  of the contestants. Moreover, no contestant solved all the
of the contestants. Moreover, no contestant solved all the 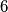 problems. Show that there are at least
problems. Show that there are at least  contestants who solved exactly
contestants who solved exactly  problems each.
problems each.
Radu Gologan and Dan Schwartz
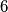 problems were posed to the participants, every two of these problems were solved by more than
problems were posed to the participants, every two of these problems were solved by more than  of the contestants. Moreover, no contestant solved all the
of the contestants. Moreover, no contestant solved all the 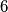 problems. Show that there are at least
problems. Show that there are at least  contestants who solved exactly
contestants who solved exactly  problems each.
problems each. Radu Gologan and Dan Schwartz
In a mathematical competition some competitors are friends. Friendship is always mutual. Call a group of competitors a clique if each two of them are friends. (In particular, any group of fewer than two competitiors is a clique.) The number of members of a clique is called its size.
Given that, in this competition, the largest size of a clique is even, prove that the competitors can be arranged into two rooms such that the largest size of a clique contained in one room is the same as the largest size of a clique contained in the other room.
Author: Vasily Astakhov, Russia
Given that, in this competition, the largest size of a clique is even, prove that the competitors can be arranged into two rooms such that the largest size of a clique contained in one room is the same as the largest size of a clique contained in the other room.
Author: Vasily Astakhov, Russia
Let 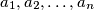 be distinct positive integers and let
be distinct positive integers and let  be a set of
be a set of 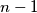 positive integers not containing
positive integers not containing 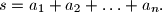 A grasshopper is to jump along the real axis, starting at the point
A grasshopper is to jump along the real axis, starting at the point  and making
and making  jumps to the right with lengths
jumps to the right with lengths 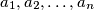 in some order. Prove that the order can be chosen in such a way that the grasshopper never lands on any point in
in some order. Prove that the order can be chosen in such a way that the grasshopper never lands on any point in 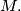
Proposed by Dmitry Khramtsov, Russia
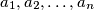 be distinct positive integers and let
be distinct positive integers and let  be a set of
be a set of 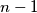 positive integers not containing
positive integers not containing 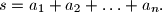 A grasshopper is to jump along the real axis, starting at the point
A grasshopper is to jump along the real axis, starting at the point  and making
and making  jumps to the right with lengths
jumps to the right with lengths 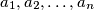 in some order. Prove that the order can be chosen in such a way that the grasshopper never lands on any point in
in some order. Prove that the order can be chosen in such a way that the grasshopper never lands on any point in 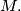
Proposed by Dmitry Khramtsov, Russia
 Školjka
Školjka  candidates and
candidates and 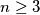 is an odd integer. Each candidate is evaluated by each judge as either pass or fail. Suppose that each pair of judges agrees on at most
is an odd integer. Each candidate is evaluated by each judge as either pass or fail. Suppose that each pair of judges agrees on at most  candidates. Prove that
candidates. Prove that 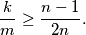
 be an even positive integer. We say that two different cells of a
be an even positive integer. We say that two different cells of a 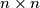 board are neighboring if they have a common side. Find the minimal number of cells on he
board are neighboring if they have a common side. Find the minimal number of cells on he