Let  be the center of the square inscribed in acute triangle
be the center of the square inscribed in acute triangle  with two vertices of the square on side
with two vertices of the square on side  . Thus one of the two remaining vertices of the square is on side
. Thus one of the two remaining vertices of the square is on side  and the other is on
and the other is on  . Points
. Points 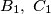 are defined in a similar way for inscribed squares with two vertices on sides
are defined in a similar way for inscribed squares with two vertices on sides  and
and  , respectively. Prove that lines
, respectively. Prove that lines 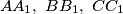 are concurrent.
are concurrent.
 be the center of the square inscribed in acute triangle
be the center of the square inscribed in acute triangle  with two vertices of the square on side
with two vertices of the square on side  . Thus one of the two remaining vertices of the square is on side
. Thus one of the two remaining vertices of the square is on side  and the other is on
and the other is on  . Points
. Points 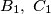 are defined in a similar way for inscribed squares with two vertices on sides
are defined in a similar way for inscribed squares with two vertices on sides  and
and  , respectively. Prove that lines
, respectively. Prove that lines 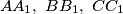 are concurrent.
are concurrent.  Školjka
Školjka