IMO Shortlist 2007 problem G2
Dodao/la:
arhiva2. travnja 2012. Denote by

midpoint of side

in an isosceles triangle

with
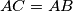
. Take a point

on a smaller arc
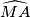
of circumcircle of triangle
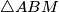
. Denote by

point inside of angle
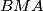
such that
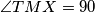
and
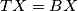
.
Prove that
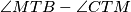
does not depend on choice of

.
Author: unknown author, Canada
%V0
Denote by $M$ midpoint of side $BC$ in an isosceles triangle $\triangle ABC$ with $AC = AB$. Take a point $X$ on a smaller arc $\widehat{MA}$ of circumcircle of triangle $\triangle ABM$. Denote by $T$ point inside of angle $BMA$ such that $\angle TMX = 90$ and $TX = BX$.
Prove that $\angle MTB - \angle CTM$ does not depend on choice of $X$.
Author: unknown author, Canada
Izvor: Međunarodna matematička olimpijada, shortlist 2007