Consider an acute-angled triangle

. Let

be the foot of the altitude of triangle

issuing from the vertex

, and let

be the circumcenter of triangle

. Assume that
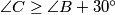
. Prove that
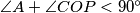
.
%V0
Consider an acute-angled triangle $ABC$. Let $P$ be the foot of the altitude of triangle $ABC$ issuing from the vertex $A$, and let $O$ be the circumcenter of triangle $ABC$. Assume that $\angle C \geq \angle B+30^{\circ}$. Prove that $\angle A+\angle COP < 90^{\circ}$.