IMO Shortlist 2005 problem G2
Dodao/la:
arhiva2. travnja 2012. Six points are chosen on the sides of an equilateral triangle

:

,

on

,

,

on

and

,
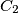
on

, such that they are the vertices of a convex hexagon
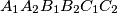
with equal side lengths.
Prove that the lines
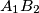
,
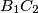
and
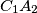
are concurrent.
Bogdan Enescu, Romania
%V0
Six points are chosen on the sides of an equilateral triangle $ABC$: $A_1$, $A_2$ on $BC$, $B_1$, $B_2$ on $CA$ and $C_1$, $C_2$ on $AB$, such that they are the vertices of a convex hexagon $A_1A_2B_1B_2C_1C_2$ with equal side lengths.
Prove that the lines $A_1B_2$, $B_1C_2$ and $C_1A_2$ are concurrent.
Bogdan Enescu, Romania
Izvor: Međunarodna matematička olimpijada, shortlist 2005