Slični zadaci
Point  lies on side
lies on side  of a convex quadrilateral
of a convex quadrilateral  . Let
. Let  be the incircle of triangle
be the incircle of triangle 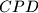 , and let
, and let  be its incenter. Suppose that
be its incenter. Suppose that  is tangent to the incircles of triangles
is tangent to the incircles of triangles 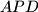 and
and 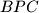 at points
at points  and
and  , respectively. Let lines
, respectively. Let lines  and
and  meet at
meet at  , and let lines
, and let lines 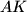 and
and 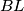 meet at
meet at  . Prove that points
. Prove that points  ,
,  , and
, and  are collinear.
are collinear.
Author: Waldemar Pompe, Poland
 lies on side
lies on side  of a convex quadrilateral
of a convex quadrilateral  . Let
. Let  be the incircle of triangle
be the incircle of triangle 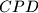 , and let
, and let  be its incenter. Suppose that
be its incenter. Suppose that  is tangent to the incircles of triangles
is tangent to the incircles of triangles 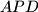 and
and 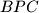 at points
at points  and
and  , respectively. Let lines
, respectively. Let lines  and
and  meet at
meet at  , and let lines
, and let lines 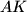 and
and 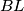 meet at
meet at  . Prove that points
. Prove that points  ,
,  , and
, and  are collinear.
are collinear. Author: Waldemar Pompe, Poland
 Školjka
Školjka  be an interior point of acute triangle
be an interior point of acute triangle  . Let
. Let  lie on
lie on  with
with 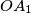 perpendicular to
perpendicular to  on
on  and
and  on
on 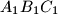 is not less than any one of the perimeters of
is not less than any one of the perimeters of 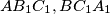 , and
, and 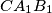 .
. 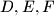 of an equilateral triangle lie on the sides
of an equilateral triangle lie on the sides 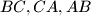 respectively of a triangle
respectively of a triangle  If
If  are the respective lengths of these sides, and
are the respective lengths of these sides, and  the area of
the area of 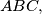 prove that
prove that 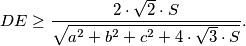
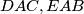 , and
, and 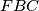 be isosceles triangles exterior to
be isosceles triangles exterior to 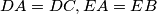 , and
, and 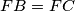 , such that
, such that 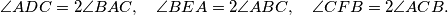
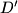 be the intersection of lines
be the intersection of lines 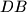 and
and  , let
, let 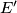 be the intersection of
be the intersection of 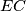 and
and 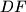 , and let
, and let 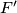 be the intersection of
be the intersection of 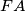 and
and 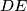 . Find, with proof, the value of the sum
. Find, with proof, the value of the sum 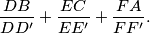
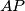 ,
, 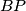 ,
, 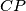 meet the sides
meet the sides  ,
, 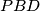 ,
, 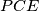 ,
, 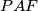 are all equal. Prove that each of these areas is equal to the area of triangle
are all equal. Prove that each of these areas is equal to the area of triangle  ,
,  and
and  be the incenters of the triangles
be the incenters of the triangles 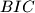 ,
, 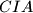 and
and 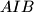 , respectively. Let the triangle
, respectively. Let the triangle 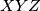 be equilateral. Prove that
be equilateral. Prove that  be a line through
be a line through  which meets the segment
which meets the segment  and the line
and the line  in
in  . Denote by
. Denote by 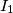 ,
, 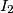 and
and 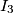 the incenters of
the incenters of 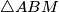 ,
, 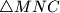 and
and 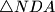 , respectively. Prove that the orthocenter of
, respectively. Prove that the orthocenter of 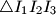 lies on
lies on