Find all functions
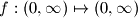
(so

is a function from the positive real numbers) such that
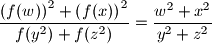
for all positive real numbes
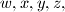
satisfying
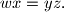
Author: Hojoo Lee, South Korea
%V0
Find all functions $f: (0, \infty) \mapsto (0, \infty)$ (so $f$ is a function from the positive real numbers) such that
$$\frac {\left( f(w) \right)^2 + \left( f(x) \right)^2}{f(y^2) + f(z^2) } = \frac {w^2 + x^2}{y^2 + z^2}$$
for all positive real numbes $w,x,y,z,$ satisfying $wx = yz.$
Author: Hojoo Lee, South Korea