For  an odd positive integer, the unit squares of an
an odd positive integer, the unit squares of an 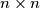 chessboard are coloured alternately black and white, with the four corners coloured black. A it tromino is an
chessboard are coloured alternately black and white, with the four corners coloured black. A it tromino is an  -shape formed by three connected unit squares. For which values of
-shape formed by three connected unit squares. For which values of  is it possible to cover all the black squares with non-overlapping trominos? When it is possible, what is the minimum number of trominos needed?
is it possible to cover all the black squares with non-overlapping trominos? When it is possible, what is the minimum number of trominos needed?
 an odd positive integer, the unit squares of an
an odd positive integer, the unit squares of an 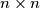 chessboard are coloured alternately black and white, with the four corners coloured black. A it tromino is an
chessboard are coloured alternately black and white, with the four corners coloured black. A it tromino is an  -shape formed by three connected unit squares. For which values of
-shape formed by three connected unit squares. For which values of  is it possible to cover all the black squares with non-overlapping trominos? When it is possible, what is the minimum number of trominos needed?
is it possible to cover all the black squares with non-overlapping trominos? When it is possible, what is the minimum number of trominos needed?  Školjka
Školjka