Let  be a positive integer. A sequence of
be a positive integer. A sequence of  positive integers (not necessarily distinct) is called full if it satisfies the following condition: for each positive integer
positive integers (not necessarily distinct) is called full if it satisfies the following condition: for each positive integer 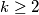 , if the number
, if the number  appears in the sequence then so does the number
appears in the sequence then so does the number 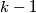 , and moreover the first occurrence of
, and moreover the first occurrence of 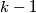 comes before the last occurrence of
comes before the last occurrence of  . For each
. For each  , how many full sequences are there ?
, how many full sequences are there ?
 be a positive integer. A sequence of
be a positive integer. A sequence of  positive integers (not necessarily distinct) is called full if it satisfies the following condition: for each positive integer
positive integers (not necessarily distinct) is called full if it satisfies the following condition: for each positive integer 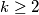 , if the number
, if the number  appears in the sequence then so does the number
appears in the sequence then so does the number 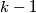 , and moreover the first occurrence of
, and moreover the first occurrence of 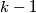 comes before the last occurrence of
comes before the last occurrence of  . For each
. For each  , how many full sequences are there ?
, how many full sequences are there ?  Školjka
Školjka