Let

be an even positive integer. Show that there is a permutation
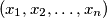
of
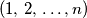
such that for every
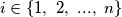
, the number
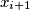
is one of the numbers
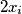
,
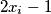
,
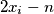
,
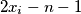
. Hereby, we use the cyclic subscript convention, so that
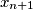
means
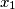
.
%V0
Let $n$ be an even positive integer. Show that there is a permutation $\left(x_{1},x_{2},\ldots,x_{n}\right)$ of $\left(1,\,2,\,\ldots,n\right)$ such that for every $i\in\left\{1,\ 2,\ ...,\ n\right\}$, the number $x_{i+1}$ is one of the numbers $2x_{i}$, $2x_{i}-1$, $2x_{i}-n$, $2x_{i}-n-1$. Hereby, we use the cyclic subscript convention, so that $x_{n+1}$ means $x_{1}$.