Circles
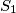
and
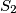
intersect at points

and

. Distinct points
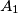
and
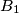
(not at

or

) are selected on
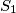
. The lines
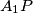
and
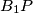
meet
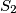
again at
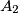
and
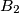
respectively, and the lines
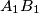
and
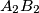
meet at

. Prove that, as
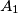
and
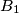
vary, the circumcentres of triangles
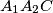
all lie on one fixed circle.
%V0
Circles $S_1$ and $S_2$ intersect at points $P$ and $Q$. Distinct points $A_1$ and $B_1$ (not at $P$ or $Q$) are selected on $S_1$. The lines $A_1P$ and $B_1P$ meet $S_2$ again at $A_2$ and $B_2$ respectively, and the lines $A_1B_1$ and $A_2B_2$ meet at $C$. Prove that, as $A_1$ and $B_1$ vary, the circumcentres of triangles $A_1A_2C$ all lie on one fixed circle.