Let
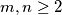
be positive integers, and let
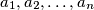
be integers, none of which is a multiple of
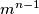
. Show that there exist integers
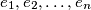
, not all zero, with
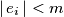
for all

, such that
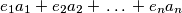
is a multiple of
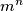
.
%V0
Let $m,n\geq2$ be positive integers, and let $a_1,a_2,\ldots ,a_n$ be integers, none of which is a multiple of $m^{n-1}$. Show that there exist integers $e_1,e_2,\ldots,e_n$, not all zero, with $\left|{\,e}_i\,\right|<m$ for all $i$, such that $e_1a_1+e_2a_2+\,\ldots\,+e_na_n$ is a multiple of $m^n$.