Slični zadaci
Let  be the set of all pairs
be the set of all pairs 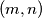 of relatively prime positive integers
of relatively prime positive integers 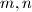 with
with  even and
even and 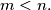 For
For 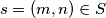 write
write 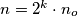 where
where 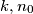 are positive integers with
are positive integers with 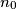 odd and define
odd and define 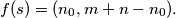 Prove that
Prove that  is a function from
is a function from  to
to  and that for each
and that for each 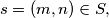 there exists a positive integer
there exists a positive integer 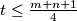 such that
such that 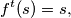 where
where 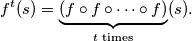
If is a prime number which does not divide
is a prime number which does not divide 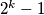 for
for 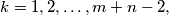 prove that the smallest value
prove that the smallest value  which satisfies the above conditions is
which satisfies the above conditions is ![\left [\frac{m+n+1}{4} \right ]](/media/m/8/7/8/878d7261cbd40fe8c838d36d2b94fea7.png) where
where ![\left[ x \right]](/media/m/8/4/7/847a3b7449538c2b99179a2953e7f9e0.png) denotes the greatest integer
denotes the greatest integer 
 be the set of all pairs
be the set of all pairs 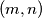 of relatively prime positive integers
of relatively prime positive integers 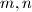 with
with  even and
even and 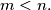 For
For 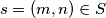 write
write 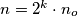 where
where 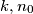 are positive integers with
are positive integers with 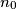 odd and define
odd and define 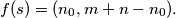 Prove that
Prove that  is a function from
is a function from  to
to  and that for each
and that for each 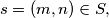 there exists a positive integer
there exists a positive integer 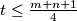 such that
such that 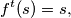 where
where 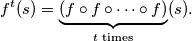
If
 is a prime number which does not divide
is a prime number which does not divide 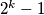 for
for 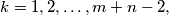 prove that the smallest value
prove that the smallest value  which satisfies the above conditions is
which satisfies the above conditions is ![\left [\frac{m+n+1}{4} \right ]](/media/m/8/7/8/878d7261cbd40fe8c838d36d2b94fea7.png) where
where ![\left[ x \right]](/media/m/8/4/7/847a3b7449538c2b99179a2953e7f9e0.png) denotes the greatest integer
denotes the greatest integer 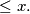
Consider two monotonically decreasing sequences  and
and  , where
, where  , and
, and 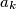 and
and 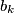 are positive real numbers for every k. Now, define the sequences
are positive real numbers for every k. Now, define the sequences
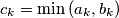 ;
;
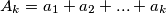 ;
;
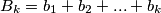 ;
;
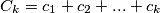
for all natural numbers k.
(a) Do there exist two monotonically decreasing sequences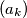 and
and  of positive real numbers such that the sequences
of positive real numbers such that the sequences 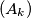 and
and 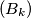 are not bounded, while the sequence
are not bounded, while the sequence 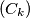 is bounded?
is bounded?
(b) Does the answer to problem (a) change if we stipulate that the sequence must be
must be 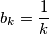 for all k ?
for all k ?
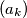 and
and  , where
, where 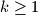 , and
, and 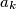 and
and 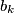 are positive real numbers for every k. Now, define the sequences
are positive real numbers for every k. Now, define the sequences 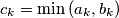 ;
; 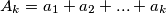 ;
; 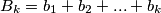 ;
; 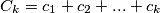
for all natural numbers k.
(a) Do there exist two monotonically decreasing sequences
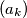 and
and  of positive real numbers such that the sequences
of positive real numbers such that the sequences 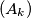 and
and 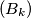 are not bounded, while the sequence
are not bounded, while the sequence 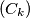 is bounded?
is bounded? (b) Does the answer to problem (a) change if we stipulate that the sequence
 must be
must be 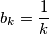 for all k ?
for all k ? Each positive integer  is subjected to the following procedure, yielding the number
is subjected to the following procedure, yielding the number 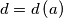 :
:
(a) The last digit of is moved to the first position. The resulting number is called
is moved to the first position. The resulting number is called  .
.
(b) The number is squared. The resulting number is called
is squared. The resulting number is called  .
.
(c) The first digit of is moved to the last position. The resulting number is called
is moved to the last position. The resulting number is called  .
.
(All numbers are considered in the decimal system.) For instance,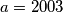 gives
gives 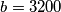 ,
, 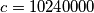 and
and 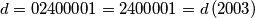 .
.
Find all integers a such that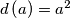 .
.
 is subjected to the following procedure, yielding the number
is subjected to the following procedure, yielding the number 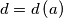 :
: (a) The last digit of
 is moved to the first position. The resulting number is called
is moved to the first position. The resulting number is called  .
. (b) The number
 is squared. The resulting number is called
is squared. The resulting number is called  .
. (c) The first digit of
 is moved to the last position. The resulting number is called
is moved to the last position. The resulting number is called  .
. (All numbers are considered in the decimal system.) For instance,
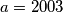 gives
gives 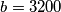 ,
, 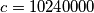 and
and 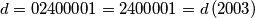 .
. Find all integers a such that
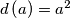 .
.  Školjka
Školjka 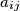 (with the indices
(with the indices  and
and  from the set
from the set 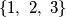 ) be real numbers such that
) be real numbers such that 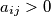 for
for 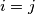 ;
; 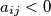 for
for 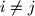 .
. 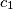 ,
, 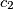 ,
, 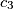 such that the numbers
such that the numbers 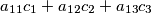 ,
, 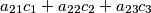 ,
, 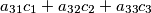
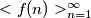 of positive integers by
of positive integers by 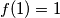 and
and 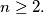 Let
Let 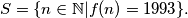
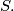
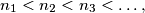 show that
show that 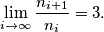
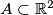 such that for every
such that for every 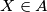 there are points
there are points 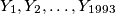 in
in  such that the distance between
such that the distance between  and
and 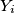 is equal to 1, for every
is equal to 1, for every 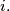
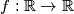 such that
such that 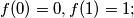
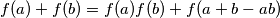 for all real numbers
for all real numbers 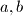 such that
such that 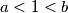 .
.