Find all nondecreasing functions
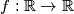
such that
(i)
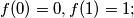
(ii)
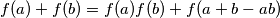
for all real numbers
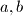
such that
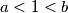
.
%V0
Find all nondecreasing functions $f: \mathbb{R}\rightarrow\mathbb{R}$ such that
(i) $f(0) = 0, f(1) = 1;$
(ii) $f(a) + f(b) = f(a)f(b) + f(a + b - ab)$ for all real numbers $a, b$ such that $a < 1 < b$.