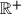
We denote by the set of all positive real numbers.
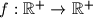
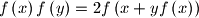
Find all functions which have the property: for all positive real numbers and .
%V0
We denote by $\mathbb{R}^+$ the set of all positive real numbers.
Find all functions $f: \mathbb R^ + \rightarrow\mathbb R^ +$ which have the property: $$f\left(x\right)f\left(y\right) = 2f\left(x + yf\left(x\right)\right)$$ for all positive real numbers $x$ and $y$.
Izvor: Međunarodna matematička olimpijada, shortlist 2005
Školjka 
the set of all positive real numbers.
which have the property: 
for all positive real numbers 
and 
.