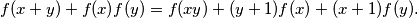Slični zadaci
Let  be an even positive integer. Prove that there exists a positive integer
be an even positive integer. Prove that there exists a positive integer  such that
such that
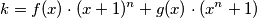
for some polynomials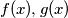 having integer coefficients. If
having integer coefficients. If 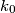 denotes the least such
denotes the least such 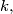 determine
determine 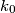 as a function of
as a function of 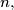 i.e. show that
i.e. show that 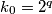 where
where  is the odd integer determined by
is the odd integer determined by 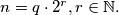
Note: This is variant A6' of the three variants given for this problem.
 be an even positive integer. Prove that there exists a positive integer
be an even positive integer. Prove that there exists a positive integer  such that
such that 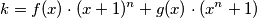
for some polynomials
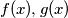 having integer coefficients. If
having integer coefficients. If 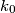 denotes the least such
denotes the least such 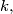 determine
determine 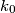 as a function of
as a function of 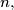 i.e. show that
i.e. show that 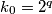 where
where  is the odd integer determined by
is the odd integer determined by 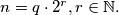
Note: This is variant A6' of the three variants given for this problem.
 Školjka
Školjka 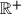 be the set of all positive real numbers. Find all functions
be the set of all positive real numbers. Find all functions 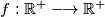 that satisfy the following conditions:
that satisfy the following conditions: 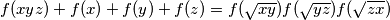 for all
for all 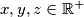 ;
; 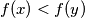 for all
for all 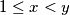 .
. 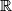 be the set of real numbers. Does there exist a function
be the set of real numbers. Does there exist a function 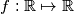 which simultaneously satisfies the following three conditions?
which simultaneously satisfies the following three conditions? such that
such that 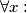
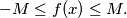
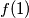 is
is  .
.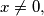 then
then![f \left(x + \frac {1}{x^2} \right) = f(x) + \left[ f \left(\frac {1}{x} \right) \right]^2](/media/m/0/c/f/0cf2538c4d8a135349370aeaece3cd1b.png)
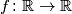 satisfying the equation
satisfying the equation 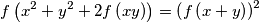 for all
for all 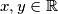 .
. 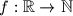 be a function which satisfies
be a function which satisfies 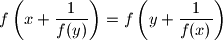 for all
for all  ,
, 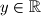 . Prove that there is a positive integer which is not a value of
. Prove that there is a positive integer which is not a value of  .
.  such that
such that 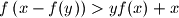
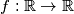 such that for all
such that for all 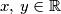 , we have
, we have