Let
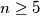
be an integer. Find the maximal integer

such that there exists a polygon with

vertices (convex or not, but not self-intersecting!) having

internal
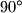
angles.
%V0
Let $n \geq 5$ be an integer. Find the maximal integer $k$ such that there exists a polygon with $n$ vertices (convex or not, but not self-intersecting!) having $k$ internal $90^{\circ}$ angles.